【冷知識週刊】第八十號：一年為什麼有 12 個月？

本文的靈感來自數感實驗室【數感生活──數字12在哪裡】一文，非常精彩，各位讀者可以點下去，讀完了再回來，我等你 :-D 快呀～

等你的過程中我又想到幾個例子：

• 歐盟的旗幟上有 12 顆金星成環狀排列，但這並不是代表創始國的數目，只是象徵團結。


• 人有 12 對腦神經，雖然這是最普遍的講法，有些人主張有十三對，有些人主張十四。


• 英國科幻劇「超時空博士」（Doctor Who）裡的外星英國人：時間領主（Time Lords）可以重生 12 次。但只有設定上是如此，主角威能，不停作弊。


• 人活到 100 歲是十乘十分的圓滿，但身為魔戒持有者，夏爾哈比屯袋底洞的比爾博．巴金斯活到了「12 個 12」即 144 歲這個更加圓滿、可以被一大堆因數整除的數字，值得請甘道夫來放煙火。

好神祕呀，啾～竟～為什麼古今中外的文化要素，會有這麼多 12 的蹤跡呢？

熟悉每日一冷的讀者也許記得，中國傳統紀年所用的十二地支是來自於「歲星」，即木星，在黃道上運行的週期大約是 12 年。但因為木星的週期並不是恰恰好等於 12，而是稍微短缺（11.8618 年），使用起來很不方便，於是古代天文官索性創造出一顆虛擬的「太歲」星，規定太歲星在天球上黃道上以與木星相反的方向，每年精準的倒退十二分之一，據此決定十二地支和黃道附近星宿的分野。也就是說，太歲是參考、脫胎自木星，卻不是木星本身。「太歲」不等於「歲星」。

這蠻厲害的，代表人類創造的計時概念「太歲」取代了實際在天上運行的木星！

那之後不久還舉辦了中原盃動物馬拉松大賽，以老鼠勝出、貓落水失格收場。

而後來在工業時代，人造的機械鐘又一次取代了太陽（日晷），作為時間的通用標準，地球上只剩下非常、非常少數的人有觀測天象的需求了。一般我們是看手錶、月曆、和氣象預報，現在通通整合在一支智慧手機裡──哪天弄丟就渾然不知道如何存活了。

※科宅補注：更詳盡的「太歲」天文學與民間信仰的考證，見泛科學『我們犯了什麼太歲？你不知道的太歲天文學』一文。

說到這順便感嘆「人若不照天理，天就不照甲子」這種穿越兩千多年時光，到今日還是很活躍的「喵電天人感應」哲學迷信，與巴比倫人更早發明的星座占卜相互輝映，是東西方神祕學之雙璧：干支和星座這兩項超級實用的資訊，總按期出現在每份報紙、社團、通訊軟體和入口網站之首頁。

〔科宅冷字典〕神祕學－

_{告訴你世上有各種匪夷所思的存在，不斷在影響你的未來。}

_{當你問：「它們是如何影響到我呢」得到回答：「不要問，很恐怖，玄之又玄你不會懂」。當你問：「要怎麼查覺到它們呢」，答：「你現在修練不夠，信心不足，先相信我，買上師開光水防身，團購有優惠數量有限要買要快。}

但是啊，如上所說，因為太歲依照定義，並不存在，所以「天」實在、真的、從來都不是「照甲子」在運行。 

大多數人忙得沒空去熟悉一下天體是怎麼走，一再接受文化圈內異口同聲的灌輸，久而久之不禁覺得「嗯嗯，跟我想的差不多」。

舉個例子，麻煩認為「月亮白天不會出來」的人舉手一下，然後哈哈大笑十二聲，笑的是讀者您自己，因為其實早晨看得到下弦月、下午看得到上弦月、新月更是在正午高掛天空（但因為日光太亮不易觀測）──都什麼時代了，「天有日月，人有陰陽」這種上古邏輯腦洞，早點破除對人類文明進展比較好。

話說我常在白天看月亮......朝會不專心。

更何況，占星星座盤上春分點在白羊座（反映出四千年前古巴比倫人看到的星空），但天文觀測用的星座盤（反映現在抬頭真正看到星空的樣子）春分點卻是在雙魚座。

造成這現象的原因是春分點退行，由於歲差，由於進動，由於木星與太陽的引力在拉扯地球這顆陀螺的啤酒肚〔參考：孫維新〕。逆看看逆看看，在哲學家的譬喻中，如鐘表般完美運行，萬古不變的天體世界，要是我們核對一下歷史──就會發現就連古希臘哲人以為完美不變的東西，都一直在變。

啊不只扯遠還偏題太遠了，另一個十二來自月亮。

話說身為剛好路過的科宅，看到上述數感實驗室的動態，心裡立刻湧現巨大衝動，覺得想推：「這裡有個好明顯的原因呀，因為月亮一年內大約繞地球 12 次......」嗯，暫停一下，好像有哪邊怪怪的。

一趟維基百科往返，左去右回之後我立刻被我自己打臉──月亮其實一年繞地球 13.368 次。這邊請自行加入日本綜藝節目的「欸？～～」音效，持續十二秒。

 從冰冷的數字來看的話

365.24 （回歸年） ÷ 27.322（月球公轉週期）＝ 13.368 次

咦？鐵的數據，怎麼和直覺完全對不起來呢。農曆一個月的天數是 29 或 30 天。那這個 27.322 天是怎麼回事？月亮你趕火車跑得快？「消失」的一個月哪裡去了，難道這世界是一個大謊言......（陷入妄想）。

好好，鎮定鎮定，事出必有因。

只消多一點調查，就會發現，原來這是因為月相週期（synodic period，就是滿月到下一次滿月之間的時間）是 29.531 天。

365.24（回歸年） ÷ 29.531（月相週期）＝ 12.368 次

即一年中有 12 次滿月，每三年會多一次， 12.368 × 3 = 37.104 有 37 次滿月：這就是「三年一閏」。

而 12.368 這個值很接近 12 又 7／19 ，這個分數有個蠻有哏的意義，那就是農曆中的置閏月的規律：「十九年七閏」。

若是家人有依傳統慶祝農曆生日，可以觀察一下，每到 19 的倍數歲──19、38、57、76、95、114 歲，農曆生日和陽曆生日會是同一天。少吃到一個蛋糕嗚嗚嗚嗚。如果不是精確同一天也會只相差一天，若仍然差很多天，那可能出生年、月、甚至日都有記錯，或是由於古早時代家裡務農需要人力，常見的故意晚報戶口，使小孩較晚入學的情形。

接下來就講到了我個人覺得最有趣的部份──月相的週期〔29.53 天〕 和月球公轉的周期〔27.32 天〕 之中神秘的差距。這個差距的成因，就和著名的面試機智問題

「時鐘時針和分針一天會重疊幾次？」

答案是 22 次，而不是直覺中的 24 次，原理完全一樣唷。

先來看地、月、日的運動究竟是怎麼樣吧。以下我們為了方便，暫且忽略月球繞地球公轉的平面（白道）實際上不在黃道面上，而且公轉軌道其實並非正圓而是橢圓形這種小事。

就是說，選擇適當的模型，逐步趨近真相，不要一次跳太快、太複雜妨礙理解。

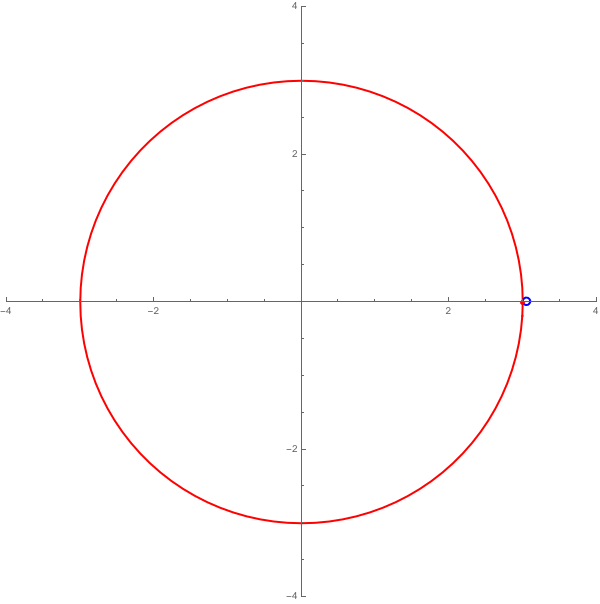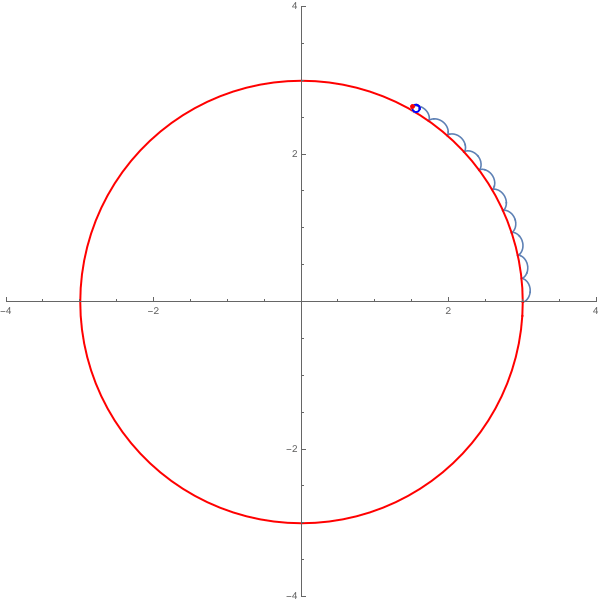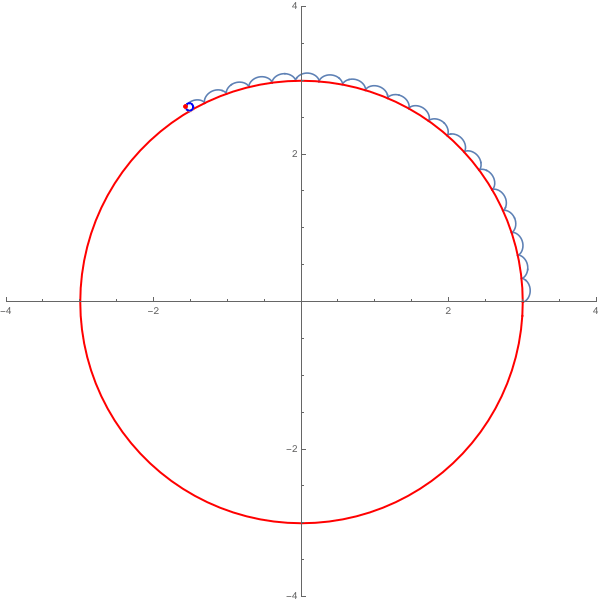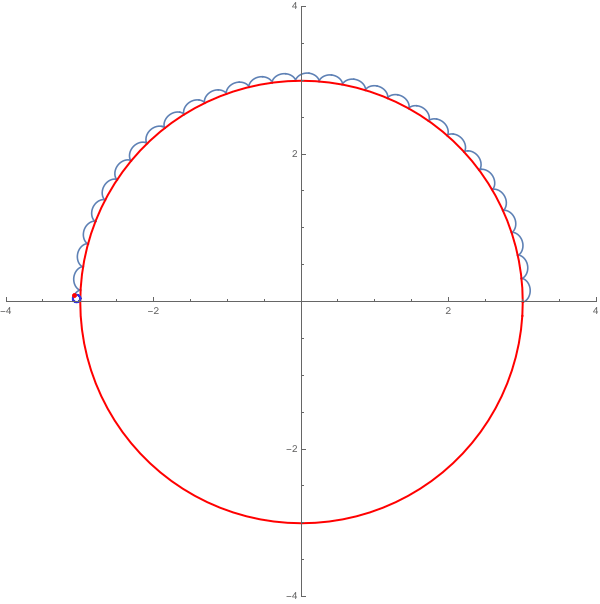
但，上面這兩個圖都不是貼切的月球軌道圖示。理由是：假設月亮的軌道真有繞圈、自我相交如上左圖，那就表示當月亮公轉到與地球的速度相反時，月亮速度比較快，想成是在機場自動步道或在手扶梯上逆著跑，必需跑得比手扶梯移動速度快才能實際上後退〔示意影片，請勿模仿，公共場所放閃太不道德〕。

而上右圖中，會形成許多尖尖的點的「花瓣」軌道，必須要月亮速度與地球完全相等，尖點處月亮相對靜止，這個軌跡稱為圓的外擺線，是用洞洞齒輪尺（萬花尺）可以畫出來的一種圖形。

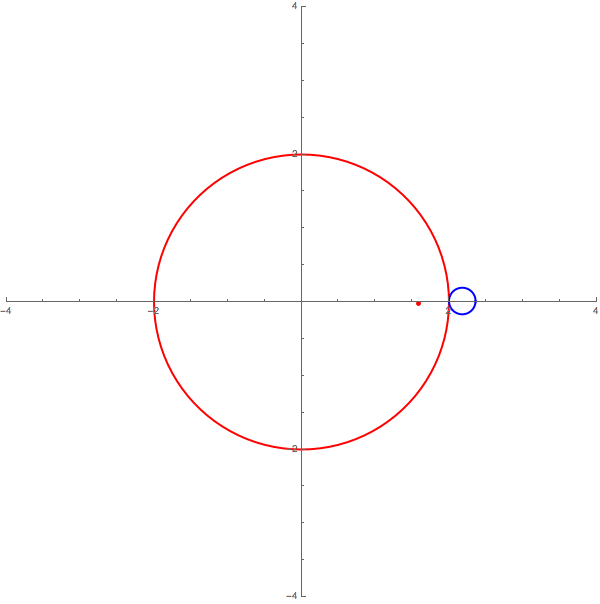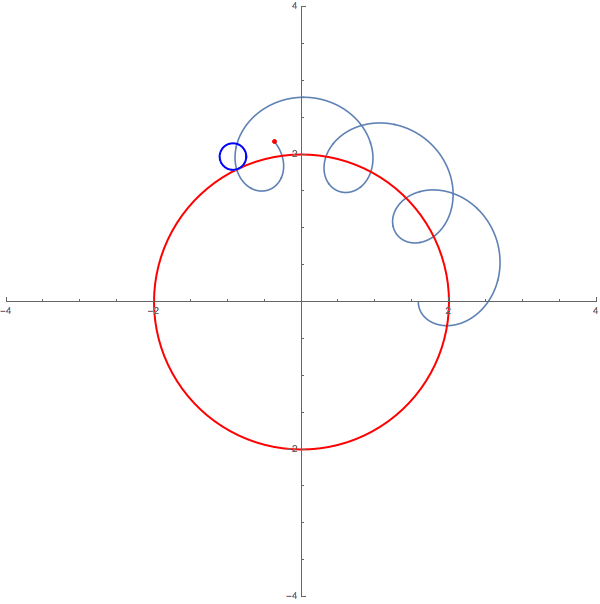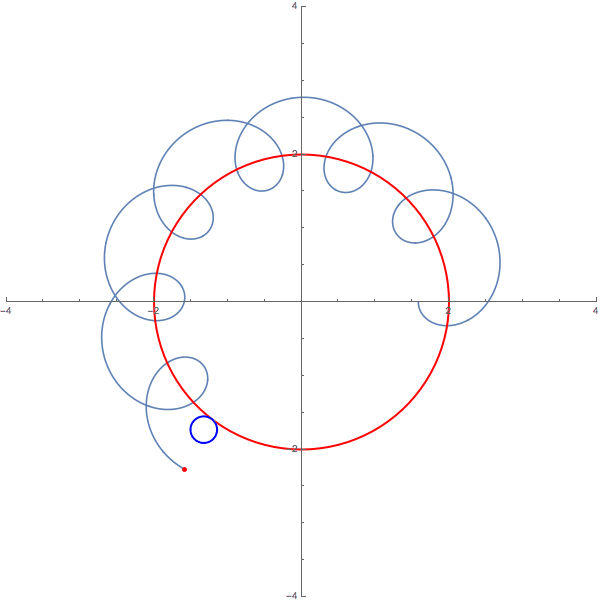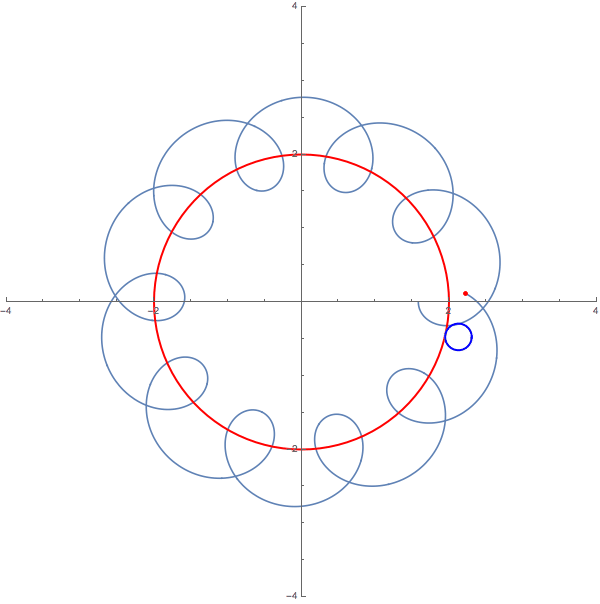
我們可以在維基百科查到地球繞太陽的軌道速度（2,575,211 公里／天），以及月亮繞地球的軌道速度（88,406 公里／天）──實際上是地球比較快，是月亮速度的 30 倍左右。

因此，完全按照比例（但忽略橢圓）的月球軌道是這樣──被速度快得多的地球拖著跑！

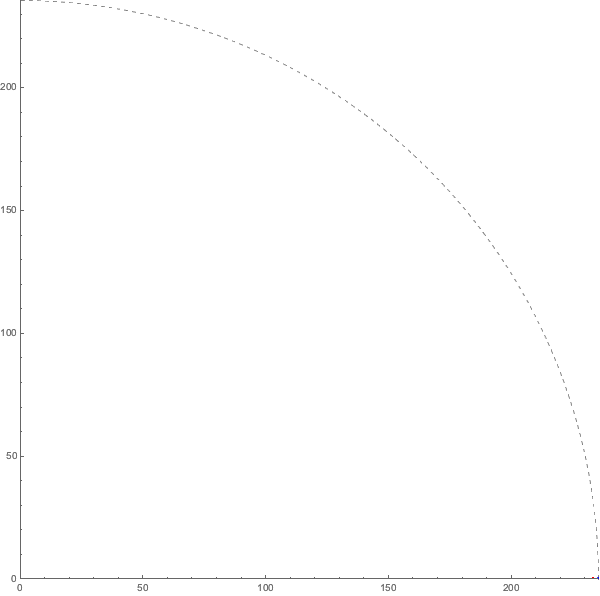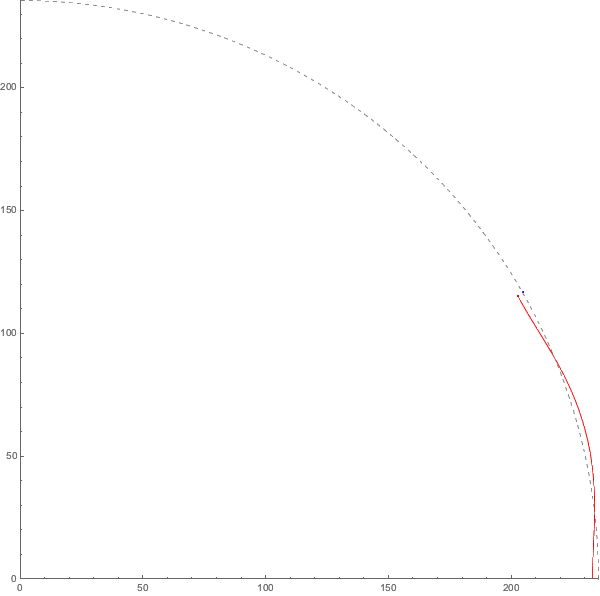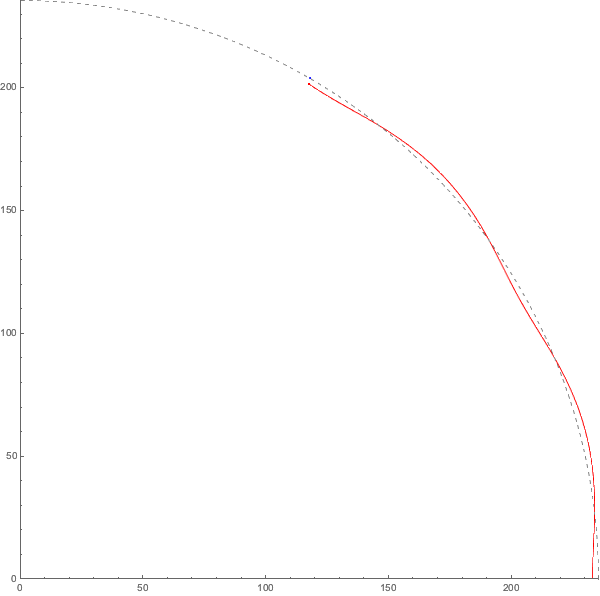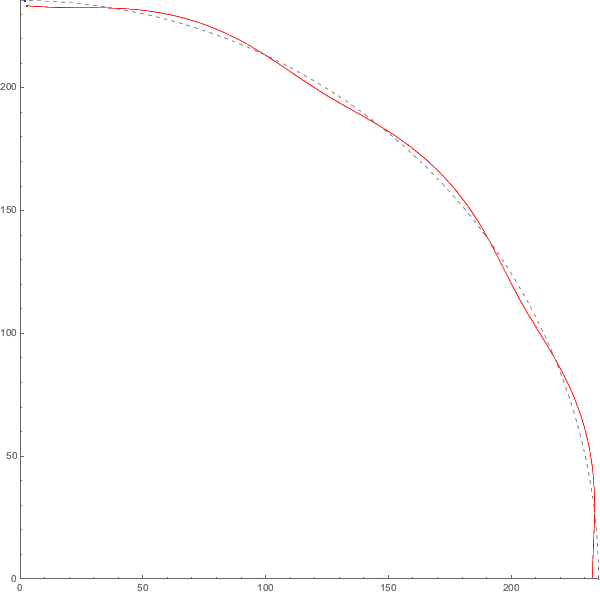
這和時鐘有什麼關係？

來你多看幾眼，不覺得時鐘很像地球、月亮、太陽嗎？
來人啊，科宅終於發瘋了

不，我是認真的，我們來想一想為什麼月有圓缺？

那是因為，月球除了月食時會被地球陰影擋到，其他時候總有半邊被太陽照到是亮的，「月相」就是我們在地球上能看到多少比例的明亮半球。

在陰曆初一，月亮在地球靠太陽的一邊，亮半球靠太陽但背向地球，我們看到的是全暗（而且如前所述，新月是清晨六點升起、傍晚六點落下，中間是大白天看不太到）。在陰曆十五，月亮在地球遠離太陽的一邊，亮半球這次朝著地球（傍晚六點升起、清晨六點落下），由我們的眼睛把正面的半球形看成一個圓。

注：這裡還有一個常搞錯的概念──不是月食時，月亮的暗半球不是地球的影子，充其量可以說是月亮自己的影子（稱為本影）就像地球的黑夜可以看成是白天的半球投下的暗影一樣，好詩，好詩。

把時鐘的時針想成地球與太陽的連線。再把分針想成月亮到地球的連線。由上面的想像我們可以發現，決定今天是月圓月缺的是這兩條連線的夾角！

而地球公轉太陽和月球公轉地球的方向一樣，所以月相的「等效角速度」等於兩者相減。

「月相的角速度」 ＝ 「月球繞地的角速度」 －「地球繞太陽的角速度」

360° ÷ 29.531 天 ＝ 360° ÷ 27.322天 － 360° ÷ 365.25 天

或 1 / 365.25 ＝ 1 / 27.322 － 1/ 29.531

你看這數字，精確得跟時鐘一樣呀，完成，收工。

科宅日冷人，我們......蛤？說明不夠清楚。好好好，應讀者要求繼續說明。

回到時鐘的例子，時針和分針的移動速度雖然和地球、月球的公轉速度不同，但我們可以類推，從「24 小時中，時針分針重疊幾次」這個機智問題來說明為什麼要扣掉－－因為這是追趕問題（六年級數學），神奇海獅被庫拉多尼追趕，一相遇神奇海獅就會被吃掉，兩人分別跳上時針與分針，這下悲劇了，不僅在非洲每過一分鐘就有 60 秒過去，在非洲分針每分鐘還會前進 360 度的 60 分之一（六十分鐘繞一圈）等於 6 度。但時針只會前進 360 度的 720 分之一（十二小時繞一圈）等於 0.5 度。每一分鐘兩人：時針與分針就會拉近 6 - 0.5 ＝ 5.5 度。

假設一開始庫拉多尼沒看到神奇海獅就在他後面，兩人相差一整圈即 360 度，只要再過 360 ÷ 5.5 = 65 又 5/11 = 720/11 分 27.3 秒，就會迎來世間最美麗味的邂逅了。

一天有 1440 分鐘，假設每吃完一隻海獅就再放一隻，一天可以吃 1440 ÷ (720/11) ＝ 22 隻。

若是機智題改成問「時針分針一天有幾次呈現直角？」那就好像在問農曆一年有幾次初七和二十二一樣，不用迷惑也不用計算，直接回答 44 次就對了。

科宅日冷人，神奇海獅好ㄘ，我們下次見。

_
對於古人怎麼用曆法馴服運轉得不是說很規律的地、月、日之關係，而且對以上冷知識程度感到輕而易舉的讀者。歡迎參考 PTT 農曆王：〈中秋適逢滿月〉一文挑戰你的腦力。

或是探討自然而然的續冷問題：一天為什麼有 24 小時？但，那又是另一個故事了。